Where I (successfully?) attempt to reverse engineer the relative weights that the website metacritic assigns to movie critics.
metacritic is a popular site that computes an aggregate metascore for each movie. The metascore is a weighted average of individual critic scores. The metacritic FAQ Page says:
Q: Can you tell me how each of the different critics are weighted in your formula?
A: Absolutely not.
That sounds like a challenge to me. Using standard machine learning/optimization techniques, we should be able to tell what critics are more important than others. In fact, the same techniques should also allow us to correctly predict the metascore for any new movie (given the individual critic ratings). This post describes my attempt to build such a system.
Note: All related code is available on my github.
The Model
We introduce some notations and assumptions about the problem:
- metacritic uses ratings from \(n\) critics.
- Our data set has \(m\) movies.
- \(r_{ij}\) is the rating of movie \(i\) by critic \(j\).
This forms an \(m \times n\) matrix.
- Not all critics rate all movies! In other words, \(r_{ij}\) may not be defined for all \(i\) and \(j\).
- Where defined, the values are constrained: \(0 \leq r_{ij} \leq 100\).
- \(\theta_j\) is the relative weight (or importance) of critic \(j\)
(this is what we are trying to learn).
- There is no point in having a critic weight of \(0\) (why even consider a critic whose rating does not affect the metascore at all?).
- In light of the previous point, we constrain critic weights to be positive, i.e., \(\theta_j > 0\) for all \(j\),
- Since these weights are relative, they must add up to one, i.e., \(\sum_{j=1}^n \theta_j = 1\).
- Critic weights stay constant across movies (but may get updated over time).
- The \(n\)-dimensional vector \(\theta = (\theta_1, \theta_2, \ldots, \theta_n)\) represents a solution, a possible assignment of weights to critics.
- Due to the above constraints, the solution space of \(\theta\) forms a bounded, affine hyperplane.
- \(p_i\) is the published metascore for movie \(i\).
- These values are also constrained: \(0 \leq p_i \leq 100\) for all \(i\).
- \(y_i(\theta)\) is the predicted metascore for movie \(i\)
for a given choice of relative weights.
- We will drop the \(\theta\) when it is obvious.
- \(p = (p_1, p_2, \ldots, p_m)\) and \(y(\theta) = (y_1(\theta), y_2(\theta), \ldots, y_m(\theta))\) are vectorized forms we will use for conciseness later.
An obvious definition of \(y_i(\theta)\) is simply a weighted sum:
\[y_i(\theta) = \sum_{j=1}^n \theta_j r_{ij}.\]But there is a problem with this definition. Remember: Not all critics rate all movies. In other words, the summation above may be invalid, since not all \(r_{ij}\) values are necessarily defined. How do we deal with this incomplete matrix \(r_{ij}\)? My best guess is that metacritic normalizes the metascore over the available critic weights. For example, assume that the (excellent) movie Ex Machina has the index \(i = 4\) in our data set. Assume that only two critics, with weights \(\theta_1\) and \(\theta_2\) have currently rated this movie. We denote their ratings \(r_{41}\) and \(r_{42}\) respectively. The metascore for this movie is then
\[y_4(\theta_1, \theta_2) = \frac{\theta_1 r_{41} + \theta_2 r_{42}}{\theta_1 + \theta_2}.\]In fact, the metacritic FAQ page says they wait until a movie has at least 4 reviews before computing a metascore. So they want at least 4 defined \(r_{ij}\) values for a given \(i\). Lets define the following additional variables:
- \(r'_{ij} = r_{ij}\) if movie \(i\) is rated by critic \(j\) and \(0\) otherwise.
- \(e_{ij} = 1\) if movie \(i\) is rated by critic \(j\), and \(0\) otherwise.
Note that \(r'_{ij}\) and \(e_{ij}\) are both \(m \times n\) matrices, but unlike \(r_{ij}\), they are fully defined.
Using these, we modify the definition for \(y_i\):
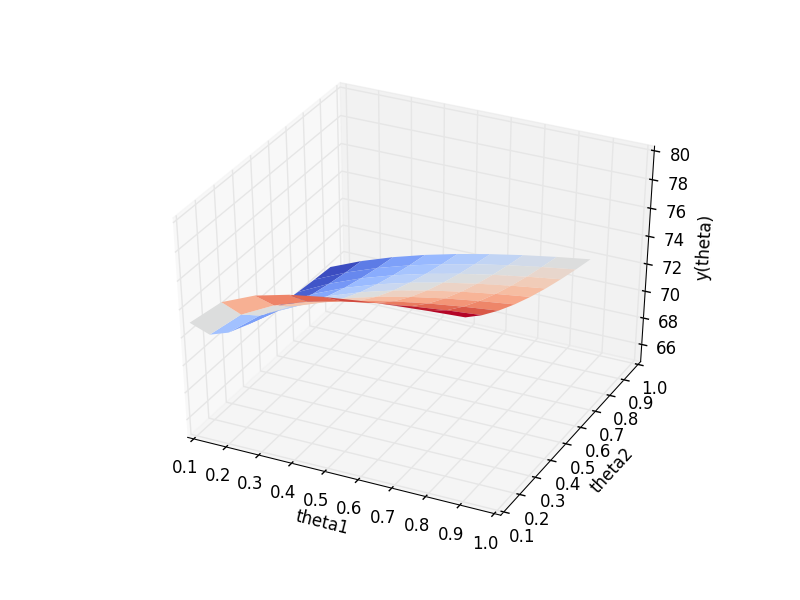
\[y_i(\theta) = \frac{ \sum_{j=1}^n \theta_j r'_{ij} }{ \sum_{j=1}^n \theta_j e_{ij} }.\]How does this function vary with \(\theta\) (once we fix the \(r_{ij}\) values)? I wrote up a little script to plot \(y_4 (\theta_1, \theta_2)\) for the example involving the movie Ex Machina (I fixed the critic ratings to \(r_{41} = 79\) and \(r_{42} = 67\); I know. Stupid critics!) The following image of the plot hopefully makes it clear that \(y_i (\theta)\) is not linear in \(\theta\). But the function is still smooth (i.e., differentiable).
Now consider the \(m\)-vector \(d(\theta) = p - y(\theta)\). This vector is a measure of how off the predictions are from actual metascores for a given \(\theta\). We will try to find a \(\theta\) that minimizes the value of the function \(f(\theta) = \Vert d(\theta) \Vert\), where \(\Vert \cdot \Vert\) represents the \(L^2\) norm. Formally,
\[\DeclareMathOperator*{\argmin}{\arg\!\min} \begin{gather*} \argmin_{\theta} \Vert p - y(\theta) \Vert \\ \text{subject to} \\ \sum_{j=1}^n \theta_j = 1, \text{and}\\ \theta_j > 0~\text{for all}~j. \end{gather*}\]This is a standard constrained minimization problem. Our expectation is that any solution \(\theta\) of the above system (a) fits the training set well, and (b) also predicts metascores for new movies. Notice that \(d\) is not a linear function of \(\theta\) because \(y(\theta)\) isn’t either. So, we have to use a nonlinear solver.
The Implementation
With (most of the) annoying math out of the way, lets write code! The implementation pipeline consists of the following stages:
- Collect movie ratings data from metacritic.
- Preprocess the data:
- Remove ratings from critics who’ve rated very few movies, and
- Create the \(r'_{ij}\) and \(e_{ij}\) matrices.
- Partition the data into a training set and a test set.
- Find a best fit \(\theta\) by running the optimization routine on the training set.
- Compute accuracy against the test set.
- Output the results.
It turns out that a Makefile is really well suited to building these kinds of pipelines, where each stage produces a file that can be used as a Make target for that stage. Each stage can be dependent on files produced in one or more previous stages.
Collecting ratings data from metacritic
Unfortunately, metacritic does not, as far as I know, have any API’s to make this data available easily. So I periodically scrape metacritic’s New Movie Releases page for links to actual metacritic movie pages, which I then scrape to get the overall metascore, and the individual critic ratings.
I used a combination of xpathtool and the lxml Python library for the scraping.
The output of this stage is a Python cPickle dump file that represents a dictionary of the form:
{ movie_url -> (metascore, individual_ratings), ... }
where individual_ratings is itself a dictionary of the form
{ critic_name -> numeric_rating, ... }.
For example, this structure could look like:
{
'http://www.metacritic.com/movie/mad-max-fury-road/critic-reviews' ->
(89,
{'Anthony Lane (The New Yorker)': 100,
'A.A. Dowd (TheWrap)': 95,
...}),
'http://www.metacritic.com/movie/ex-machina/critic-reviews' ->
(78,
{'Steven Rea (Philadelphia Inquier)': 100,
'Manohla Dargis (The New York Times)': 90,
...}),
...
}
I know cPickle is not exactly the most portable format, but it works well at this early stage. In the long run, I want to persist all of the ratings data in a database (sqlite? Postgres?).
Preprocessing
We first eliminate from our data set the long tail of critics who’ve rated very few movies. Not only are these critics not very influential to the overall optimization routine, eliminating them also helps reduce \(n\) (the matrix width). Accordingly, there is a configurable rating count threshold, currently set to \(5\). We do one pass over the ratings data and construct a dictionary of the form:
{ critic_name -> movies_rated, ... }
We then do another pass through the data and remove ratings
from critics whose movies_rated value is lower than the
threshold.
The second preprocessing step is to construct the \(r'_{ij}\) and \(e_{ij}\) matrices, which of course is a simple matter of programming. I store these values as numpy matrices.
Partitioning the data set
This is straightforward.
I use a configurable training_frac parameter
(a value in the interval \([0, 1]\)) to probabilistically
split the cleaned up data into a test set and a training
set.
Optimization routine
There are numerous “solvers” available for constrained optimization problems of the type we described above, but not all of them are freely available.
I tried the following two solvers, available as part of scipy.optimize:
| Solver | Differentiability requirements | Allows bounds? | Allows equality constraints? | Allows inequality constraints? |
|---|---|---|---|---|
| Sequential Least Squares Programming (SLSQP) | The objective function and the constraints should be twice continuously differentiable | Yes | Yes | Yes |
| Constrained Optimization By Linear Approximations (COBYLA) | None | No | No | Yes |
Note that \(y(\theta)\) (and therefore \(f(\theta)\)) satisfies the differentiability requirement of SLSQP.
Also, COBYLA does not allow you to specify bounds on \(\theta\) values or equality constraints. So, we employ a common technique in optimization formulations, which is to push the constraints into the objective function. Consider the “tub” function \(\tau(x, l, u)\) defined as:
\[\tau (x, l, u) = \begin{cases} 0 & \quad \text{if } l \leq x \leq u, \\ 1 & \quad \text{otherwise}. \end{cases}\]Our modified objective function (for use with COBYLA) becomes:
\[f(\theta) = \Vert p - y(\theta) \Vert + P_h \cdot \Vert 1 - \sum_{j=1}^n \theta_j \Vert + P_b \cdot \sum_{j = 1}^n \tau(\theta_j, 0, 1),\]where \(P_h\) and \(P_b\) are configurable weights that decide how much we should penalize the optimization algorithm when it chooses:
- a \(\theta\) that doesn’t lie on the affine hyperplane, and
- \(\theta_j\) values outside the interval \([0, 1]\),
respectively.
Setting both \(P_h\) and \(P_b\) to 0 reduces our objective function to its original form, so we can use the same function for both solvers by simply tweaking these weights.
Results
Before I actually launch into details, I should note the following issues right at the outset:
- I was actually unable to get either SLSQP or COBYLA to ever successfully converge on a solution.
- The \(\theta\) values (i.e., critic weights) learned by these solvers were often way outside the interval \([0, 1]\).
Most of the times, both routines finished their iterations and failed with errors of this form:
optimization failed [8]: Positive directional derivative for linesearch
optimization failed [2]: Maximum number of function evaluations has been exceeded
If you have experience with the numpy optimization library, I’d love to hear about suggestions you may have on how to deal with these errors.
Perhaps more interestingly, in spite of the above issues, the learned \(\theta\) values were still able to successfully predict metascores for movies in the test set.
After removing ratings from insignificant critics, I constructed a training set of about 2800 ratings of 190 movies by 188 critics.
The following table lists the top 20 critics by weight learned using the above training set with each optimization routine. Note that the weights are expressed as a percentage of the weight for the top critic in each list. Interestingly enough, both algorithms think Mike Scott of the New Orleans Times-Picayune is the metacritic MVP. So, for example, according to SLSQP, a review by Justin Lowe carries only 95% of the importance that is given to a review by Mike Scott.
| SLSQP | COBYLA | ||
|---|---|---|---|
| Weight | Critic | Weight | Critic |
| \(\cdot\) | Mike Scott (New Orleans Times-Picayune) | \(\cdot\) | Mike Scott (New Orleans Times-Picayune) |
| 0.949948 | Justin Lowe (The Hollywood Reporter) | 0.902288 | Slant Magazine |
| 0.929495 | Jordan Hoffman (The Guardian) | 0.900024 | Ronnie Scheib (Variety) |
| 0.914186 | Marjorie Baumgarten (Austin Chronicle) | 0.890113 | Wes Greene (Slant Magazine) |
| 0.910820 | Fionnuala Halligan (Screen International) | 0.887845 | Chris Cabin (Slant Magazine) |
| 0.909801 | James Mottram (Total Film) | 0.885791 | Martin Tsai (Los Angeles Times) |
| 0.904564 | Variety | 0.863626 | Lawrence Toppman (Charlotte Observer) |
| 0.903029 | Guy Lodge (Variety) | 0.858237 | Anthony Lane (The New Yorker) |
| 0.897749 | Inkoo Kang (TheWrap) | 0.845864 | Fionnuala Halligan (Screen International) |
| 0.894605 | indieWIRE | 0.834088 | Boyd van Hoeij (The Hollywood Reporter) |
| 0.892237 | Ben Kenigsberg (The New York Times) | 0.820908 | Variety |
| 0.882656 | Mike D’Angelo (The Dissolve) | 0.814152 | Nicolas Rapold (The New York Times) |
| 0.875550 | Simon Abrams (Village Voice) | 0.735623 | Justin Lowe (The Hollywood Reporter) |
| 0.875385 | Martin Tsai (Los Angeles Times) | 0.629166 | Mark Olsen (Los Angeles Times) |
| 0.875062 | Manohla Dargis (The New York Times) | 0.625141 | The Globe and Mail (Toronto) |
| 0.874889 | Kyle Smith (New York Post) | 0.567734 | James Berardinelli (ReelViews) |
| 0.872482 | Nicolas Rapold (The New York Times) | 0.562606 | Peter Sobczynski (RogerEbert.com) |
| 0.869911 | James Berardinelli (ReelViews) | 0.558980 | John Anderson (Wall Street Journal) |
| 0.863118 | Ronnie Scheib (Variety) | 0.520855 | Steve Macfarlane (Slant Magazine) |
| 0.860796 | Nikola Grozdanovic (The Playlist) | 0.510842 | Jordan Mintzer (The Hollywood Reporter) |
I should clarify that the top 20 list can change from one run to the next, since it depends on the training set chosen (which is at random).
Next, we show a few sample predicted metascores:
| Movie | Actual Metascore | Predicted (SLSQP) | Predicted (COBYLA) |
|---|---|---|---|
| Survivor | 26 | 30 (16.18%) | 33 (28.12%) |
| Entourage | 38 | 57 (50.25%) | 43 (15.65%) |
| Chappie | 41 | 46 (12.89%) | 43 (6.00%) |
| Dreamcatcher | 86 | 77 (-10.46%) | 83 (-2.77%) |
| Avengers: Age of Ultron | 66 | 62 (-5.05%) | 67 (1.57%) |
| Gemma Bovery | 57 | 0 (-100.00%) | 61 (7.15%) |
| Alleluia | 84 | 90 (7.41%) | 87 (4.13%) |
With a test set of size 60, the movie predictions by the two algorithms had the following RMSE values:
| SLSQP | COBYLA |
|---|---|
| 0.053437 | 0.016942 |
Takeaways
- Working out the math was obviously fun!
- I got to brush up on my long defunct skills with numpy, scipy, matplotlib, etc.
- Even a toy project like this one can end up demanding substantial time and attention, especially if it is something you want to share with the rest of the world. For example, I ended up setting up proper Python package management for all the code.
- Writing this blog post was also extremely useful because it clarified my own thinking on the topic. I was actually able to go back and refactor the code to better match the implementation pipeline I described above.